ΔΙΑΙΡΕΤΕΣ - ΚΟΙΝΟΙ ΔΙΑΙΡΕΤΕΣ - ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ
ΔΙΑΙΡΕΤΕΣ

ΚΟΙΝΟΙ
ΔΙΑΙΡΕΤΕΣ - ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ (Μ.Κ.Δ.)
ΠΩΣ
ΒΡΙΣΚΟΥΜΕ ΤΟΝ ΜΚΔ ΔΥΟ Ή ΠΕΡΙΣΣΟΤΕΡΩΝ ΑΡΙΘΜΩΝ
ΜΟΝΑΔΕΣ ΜΕΤΡΗΣΗΣ ΕΠΙΦΑΝΕΙΑΣ

ΜΟΝΑΔΕΣ ΜΕΤΡΗΣΗΣ ΜΗΚΟΥΣ
ΜΕΤΑΤΡΟΠΕΣ
ΜΕΤΑΤΡΟΠΗ ΕΤΕΡΩΝΥΜΩΝ
ΚΛΑΣΜΑΤΩΝ
ΣΕ ΟΜΩΝΥΜΑ
ΣΕ ΟΜΩΝΥΜΑ
Θέλω να μετατρέψω τα παρακάτω ετερώνυμα κλάσματα σε ομώνυμα.
Ακολουθώ τα εξής βήματα :
- Βρίσκω
ένα Κοινό Πολλαπλάσιο των παρονομαστών ή καλύτερα το Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.).
- Γράφω
στο ημικύκλιο (καπελάκι), πάνω από τον αριθμητή του κλάσματος, τον αριθμό
εκείνο που, αν τον πολλαπλασιάσω με τον παρονομαστή, μου δίνει το
Κοινό Πολλαπλάσιο ή το Ε.Κ.Π. (ανάλογα ποιο χρησιμοποίησα).
- Πολλαπλασιάζω
και τους δύο όρους του κλάσματος (αριθμητή και παρονομαστή) με τον αριθμό
που είναι στο "καπελάκι".
- Τα
ισοδύναμα κλάσματα που προκύπτουν έχουν τον ίδιο παρονομαστή, δηλαδή είναι
ομώνυμα.
Πώς βρίσκω το Ελάχιστο Κοινό Πολλαπλάσιο ;
Ε.Κ.Π

Πράξεις με τα κλάσματα
α)
Πρόσθεση και αφαίρεση
Για να
προσθέσω ή να αφαιρέσω κλάσματα πρέπει πρώτα να τα κάνω ομώνυμα.
Αυτό γίνεται
βρίσκοντας το Ε.Κ.Π.
Αν έχω
μεικτούς αριθμούς, προσθέτω χωριστά τους ακεραίους και χωριστά τα κλάσματα .
Αν έχω να
αφαιρέσω μεικτούς, υπάρχουν 2 τρόποι:
1) Μετατρέπω τους μεικτούς σε κλάσματα
και κάνω την αφαίρεση .
2) Αφαιρώ τον ακέραιο από τον ακέραιο και το κλάσμα από το
κλάσμα
β)
Πολλαπλασιασμός
Για
να πολλαπλασιάσουμε κλάσμα με κλάσμα, πολλαπλασιάζουμε αριθμητή με αριθμητή και
το γινόμενο το γράφουμε στον αριθμητή και παρονομαστή με παρονομαστή και το
γινόμενο το γράφουμε στον παρονομαστή.
Αν
έχω να πολλαπλασιάσω μεικτούς τους μετατρέπω πρώτα σε κλάσματα.
γ) Διαίρεση
Για
να διαιρέσουμε κλάσμα με κλάσμα, πολλαπλασιάζουμε το διαιρετέο με τον
αντίστροφο του διαιρέτη. Αν έχουμε μεικτούς τους μετατρέπουμε σε κλάσματα.
Αναγωγή στη δεκαδική κλασματική μονάδα
Κλάσματα
Κλάσματα
ΚΛΑΣΜΑΤΑ
Αριθμητής και Παρονομαστής
Κλασματικές μονάδες
Τα 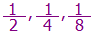 είναι κλασματικές μονάδες, γιατί κάθε φορά παίρνω ένα κομμάτι από αυτά που χώρισα (μοίρασα).
είναι κλασματικές μονάδες, γιατί κάθε φορά παίρνω ένα κομμάτι από αυτά που χώρισα (μοίρασα).
Όσο μεγαλύτερος είναι ο παρονομαστής, τόσο μικρότερο είναι το κομμάτι που θα πάρουμε.
Για παράδειγμα αν έχω δύο ίδιες σοκολάτες και χωρίσω τη μία σε δύο κομμάτια και την άλλη σε 3 κομμάτια και φάω το ένα κομμάτι από κάθε σοκολάτα θα φάω περισσότερο από την πρώτη σοκολάτα.
Κλασματική μονάδα έχω όταν παίρνω το ένα από τα ίσα μέρη στα οποία έχω χωρίσει (μοιράσει) την ακέραια μονάδα. Αριθμητής σε μια κλασματική μονάδα είναι το 1.
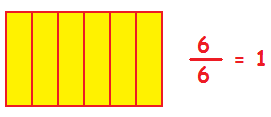 Στο διπλανό σχήμα έχουμε χρωματίσει και τα 6 κομμάτια του ορθογωνίου. Το έχουμε δηλαδή χρωματίσει όλο. Οπότε μπορούμε να πούμε ότι ισούται με τη μονάδα (1).
Στο διπλανό σχήμα έχουμε χρωματίσει και τα 6 κομμάτια του ορθογωνίου. Το έχουμε δηλαδή χρωματίσει όλο. Οπότε μπορούμε να πούμε ότι ισούται με τη μονάδα (1).

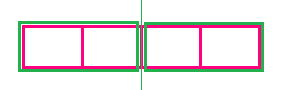

Παραδείγματα κλασματικών αριθμών:
Στο τελευταίο σχήμα παρατηρούμε ότι οι κλασματικοί αριθμοί που έχουν ίδιο αριθμητή και παρονομαστή είναι ίσοι με την ακέραια μονάδα.
Πχ:
 Στο διπλανό σχήμα έχουμε χρωματίσει και τα 6 κομμάτια του ορθογωνίου. Το έχουμε δηλαδή χρωματίσει όλο. Οπότε μπορούμε να πούμε ότι ισούται με τη μονάδα (1).
Στο διπλανό σχήμα έχουμε χρωματίσει και τα 6 κομμάτια του ορθογωνίου. Το έχουμε δηλαδή χρωματίσει όλο. Οπότε μπορούμε να πούμε ότι ισούται με τη μονάδα (1).
Προσοχή: Αν μου δώσουν ένα σχήμα σαν αυτό:

και μου πουν να χρωματίσω το 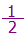 ενώ το σχήμα είναι χωρισμένο σε 4 κομμάτια θα πρέπει να σκεφτώ έναν τρόπο να το ξαναχωρίσω σε 2 κομμάτια. Δηλαδή:
ενώ το σχήμα είναι χωρισμένο σε 4 κομμάτια θα πρέπει να σκεφτώ έναν τρόπο να το ξαναχωρίσω σε 2 κομμάτια. Δηλαδή:

Έτσι θα το έχω χωρίσει σε δύο κομμάτια και θα μπορώ να χρωματίσω το 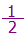 . Δηλαδή:
. Δηλαδή:

Ισοδύναμα κλάσματα
Οι κλασματικοί αριθμοί που έχουν διαφορετικό αριθμητή και διαφορετικό παρονομαστή ο ένας από τον άλλο, αλλά έχουν ίση αξία, ονομάζονται ισοδύναμα κλάσματα.
Παράδειγμα:
Και στα τρία παραπάνω όμοια σχήματα έχουμε χρωματίσει το ίδιο μέρος παρόλο που δεν έχουν τον ίδιο κλασματικό αριθμό. Έτσι λέμε ότι τα παραπάνω κλάσματα είναι ισοδύναμα και τα συμβολίζουμε έτσι:
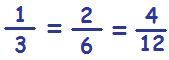
Παράδειγμα με το ευρώ
Τι μέρος του ενός ευρώ είναι 5 νομίσματα των 10 λεπτών;
Τι παρατηρούμε;
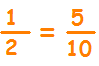
Τα παραπάνω κλάσματα είναι ισοδύναμα.

Παίξε με τα ισοδύναμα κλάσματα.. κλικ εδώ
Δημιουργώ ισοδύναμα κλάσματα πολλαπλασιάζοντας ή διαιρώντας και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό.
Όταν πολλαπλασιάζω και τους δύο όρους του κλάσματος, δημιουργώ ένα ισοδύναμο κλάσμα με μεγαλύτερους όρους.
|
Όταν διαιρώ και τους δύο όρους του κλάσματος
με τον ίδιο αριθμό, δημιουργώ ένα ισοδύναμο κλάσμα με μικρότερους όρους.
Η διαδικασία αυτή ονομάζεται απλοποίηση
(το κλάσμα γίνεται πιο απλό).
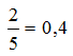
(το κλάσμα γίνεται πιο απλό).
Μετατροπές
Για να μετατρέψουμε ένα κλάσμα σε δεκαδικό αριθμό, διαιρούμε τον αριθμητή με τον παρονομαστή.
Παράδειγμα
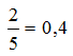
Αν μια διαίρεση δε δίνει ακριβές πηλίκο, τότε υπολογίζουμε το πηλίκο κατά προσέγγιση (περίπου) και σταματάμε στα χιλιοστά.
Παράδειγμα






























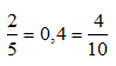


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου